Authors: Aditya Mohan, Carolin Benjamins, Konrad Wienecke, Alexander Dockhorn, and Marius Lindauer
TL;DR: We investigate hyperparameters in RL by building landscapes of algorithm performance for different hyperparameter values at different stages of training. Using these landscapes, we empirically demonstrate that adjusting hyperparameters during training can improve performance, which opens up new avenues to build better dynamic optimizers for RL.
Reinforcement Learning has been making waves with its impressive performance across various domains [1,2,3]. Yet, one stumbling block has been the significant impact of hyperparameters on RL algorithm success. Manual tuning of these hyperparameters can be arduous and is not always optimal. This is where Automated RL (AutoRL) comes into play, aiming to automate this process, with hyperparameter optimization (HPO) being one of its central pillars.
While AutoRL has shown promise, there is still a lack of understanding of how different hyperparameter configurations evolve over time and whether or not there is even a need to change them during training. To address this, we introduce hyperparameter landscapes for Reinforcement Learning.
Instead of a single snapshot of hyperparameter configuration, we view hyperparameters as evolving entities across the training process.
The figure below shows an overview of our approach for a minimal example of three hyperparameters.

Our approach to building the snapshots of landscapes involves the following key steps:
- We divide the training into three phases at $t_{ls(1)}, t_{ls(2)}, t_{final}$.
- In each phase, we sample a bunch of hyperparameter configurations using Sobol sampling [4] and run them till the end of the phase and storing their performance values at the end of the phase
- We use the final performance of each configuration to obtain the best configuration that can be fed to the sobol sampler.
To ensure sufficient coverage, we build these landscapes for algorithms that cover three very different ways of optimization in RL, including Deep Q-Network (DQN) [5], Proximal Policy Optimization (PPO) [6], and Soft Actor-Critic (SAC) [7], and evaluate these algorithms on environments with very different dynamics such as Cartpole, Bipedal Walker, and Hopper [8].
Our empirical shows that hyperparameters evolve and shape-shift as the training progresses.
The figures below show some of the landscapes we built for DQN, PPO, and SAC.
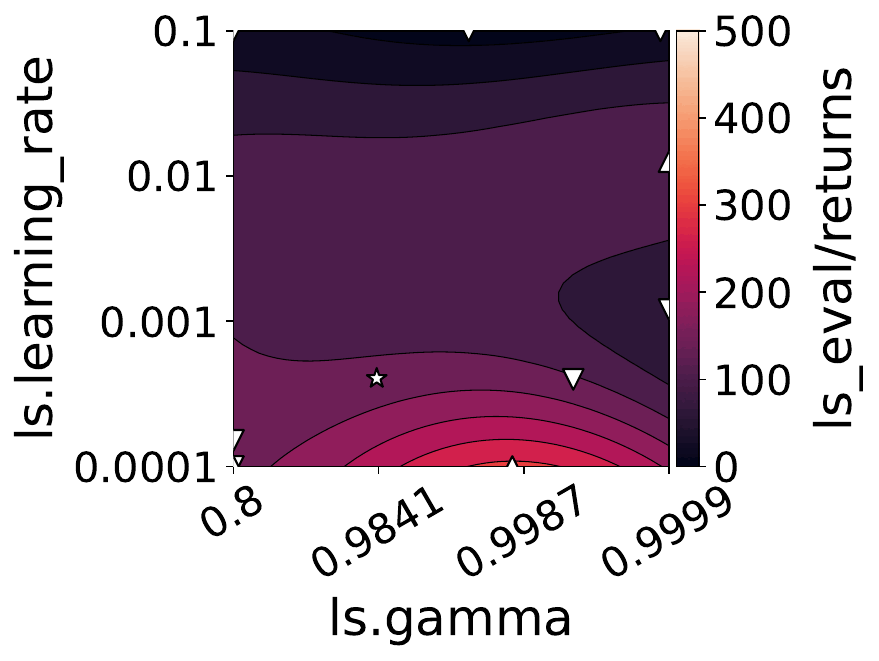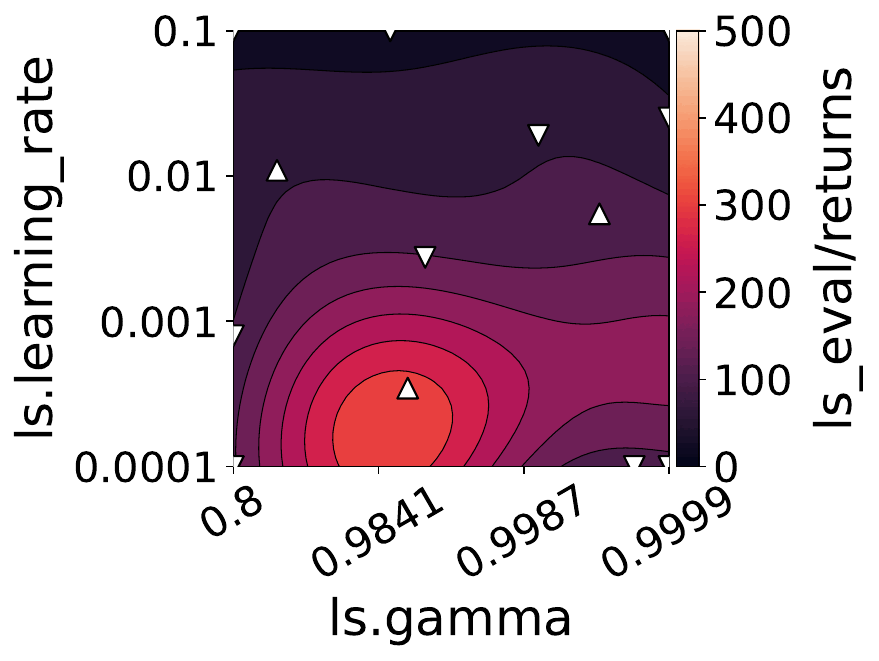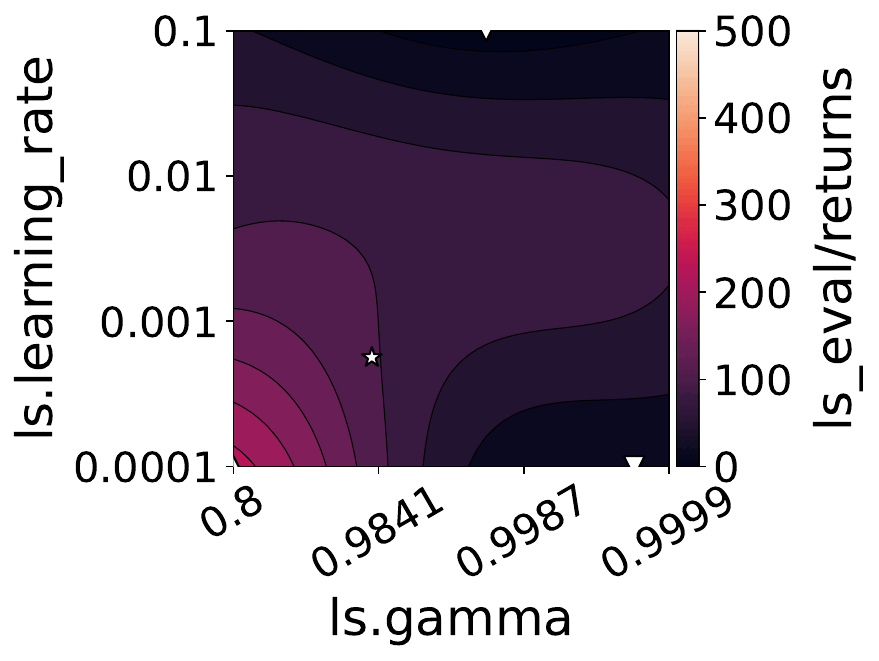
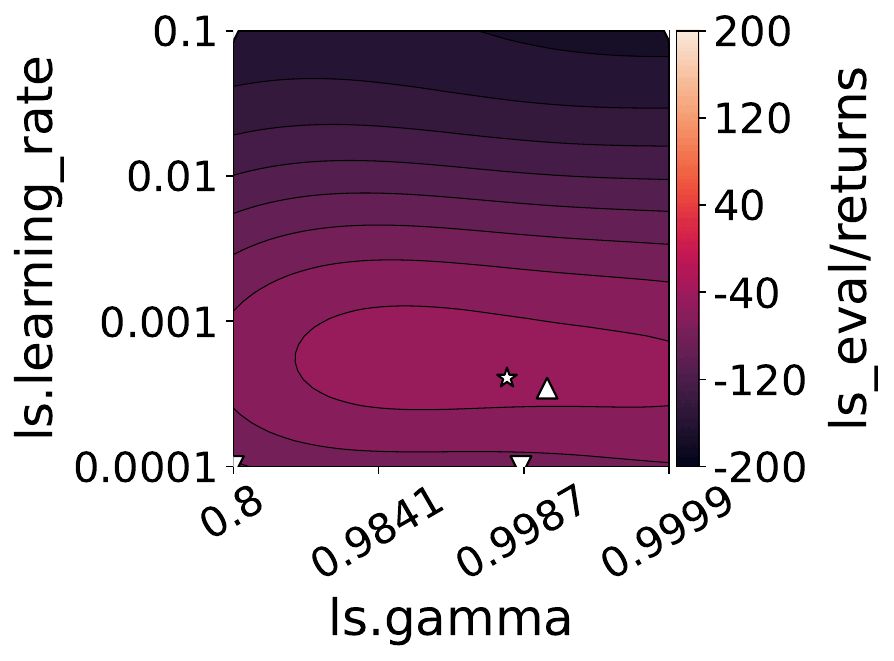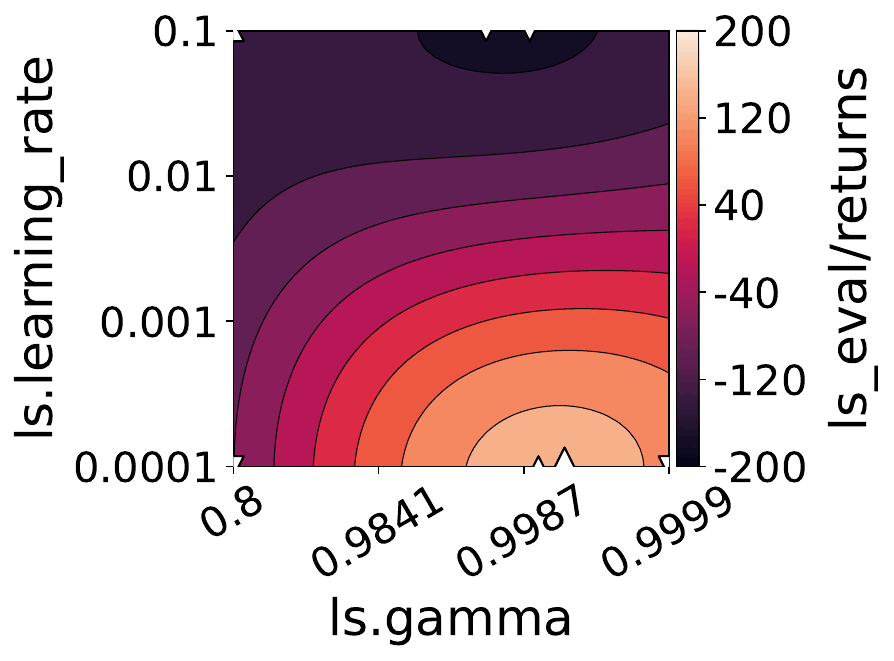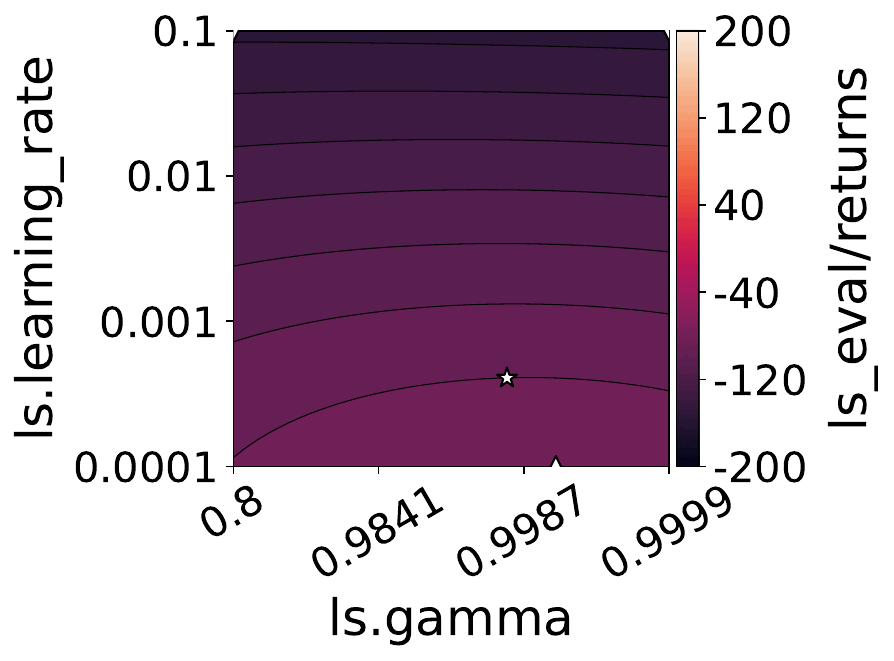
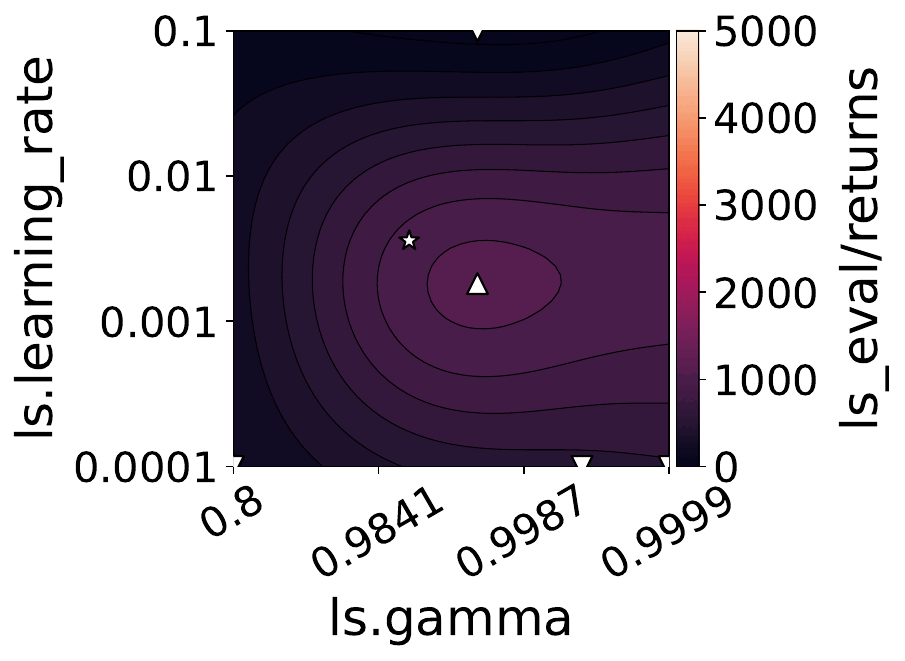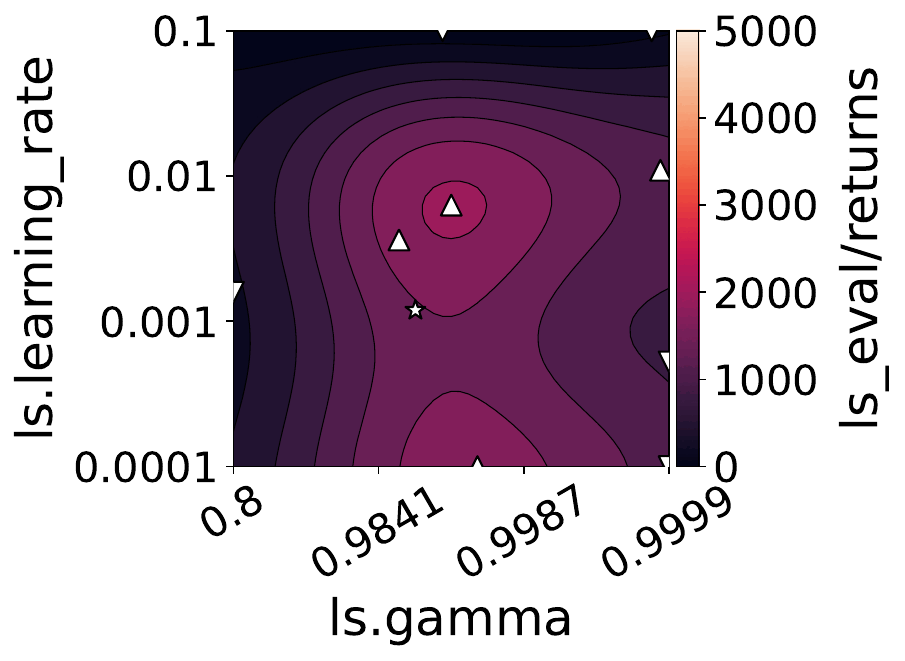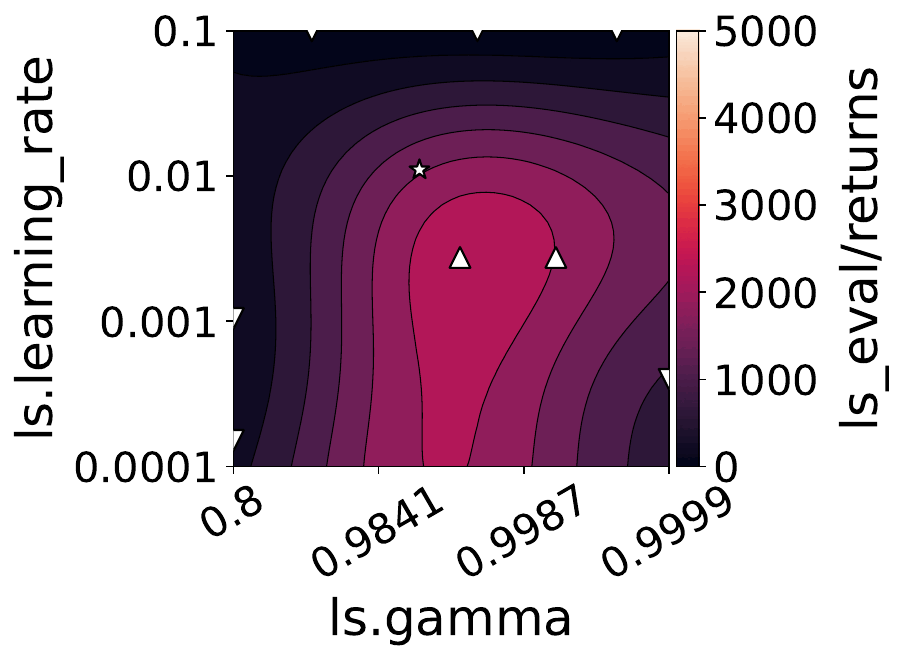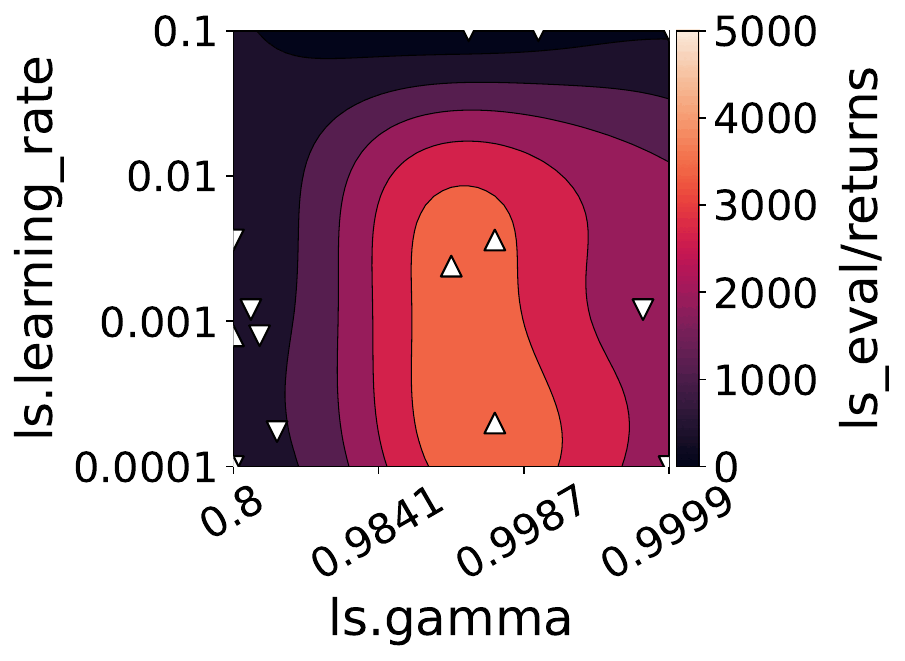
What does this mean for the performance of your RL algorithms?
Quite a lot, as it turns out!
- Our results suggest dynamically adjusting hyperparameters during training can improve performance. Thus, AutoRL approaches that adaptively optimize hyperparameters throughout the learning process would potentially fare better than static approaches that only consider earlier snapshots of training.
- What about Multi-fidelity methods that try to use performance estimates at earlier training points to predict final performance? It might not be so straightforward to apply them directly to RL problems.
- It might just be possible to build optimizers that are better suited for RL by capturing this changing nature of the landscape.
We believe that our work opens the doors to many more interesting analyses that can be performed on RL algorithms, examining the interplay between hyperparameters and the dynamics of how different RL algorithms fundamentally learn in different settings.
If we did catch your attention and you feel motivated to check out our work, here are links to our paper and our repository!
References
[1] Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., … & Hassabis, D. (2016). Mastering the game of Go with deep neural networks and tree search. nature, 529(7587), 484-489.
[2] Degrave, J., Felici, F., Buchli, J., Neunert, M., Tracey, B., Carpanese, F., … & Riedmiller, M. (2022). Magnetic control of tokamak plasmas through deep reinforcement learning. Nature, 602(7897), 414-419.
[3] Lee, J., Hwangbo, J., Wellhausen, L., Koltun, V., & Hutter, M. (2020). Learning quadrupedal locomotion over challenging terrain. Science robotics, 5(47), eabc5986.
[4] Sobol’, I. Y. M. (1967). On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 7(4), 784-802.
[5] Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., … & Hassabis, D. (2015). Human-level control through deep reinforcement learning. nature, 518(7540), 529-533.
[6] Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
[7] Haarnoja, T., Zhou, A., Hartikainen, K., Tucker, G., Ha, S., Tan, J., … & Levine, S. (2018). Soft actor-critic algorithms and applications. arXiv preprint arXiv:1812.05905.
[8] Brockman, G., Cheung, V., Pettersson, L., Schneider, J., Schulman, J., Tang, J., & Zaremba, W. (2016). Openai gym. arXiv preprint arXiv:1606.01540.