Authors: Jörg Franke, Michael Hefenbrock, Gregor Koehler, Frank Hutter
Introduction
We present in our recent preprint a novel approach to parameter regularization for deep learning: Constrained Parameter Regularization (CPR). It is an alternative to traditional weight decay. Instead of applying a constant penalty uniformly to all parameters, we enforce an upper bound on a statistical measure (e.g., the L2-norm) of individual parameter groups. This reformulates learning as a constrained optimization problem. To solve this, we utilize an adaptation of the augmented Lagrangian method. Our approach allows for varying regularization strengths across different parameter groups, removing the need for explicit penalty coefficients in the regularization terms.
CPR only requires two hyperparameters, one of which can be fixed to 1.0, and introduces no measurable runtime overhead. We offer empirical evidence of CPR’s effectiveness through experiments in the “grokking” phenomenon, image classification, and language modeling. Our findings show that CPR can counteract the effects of grokking, and it consistently matches or surpasses the performance of traditional weight decay.
The CPR Algorithm
CPR operates by enforcing an upper limit on the statistical measures (e.g. L2-norm) of parameter groups (e.g. a weight matrix). This process turns the learning procedure into a constrained optimization problem, solved via an adaptation of the augmented Lagrangian method. This method allows to dynamically adjust the penalty coefficients individually for different parameter groups which violates the constraints (kappa) to the statistical measure. We present three different methods to initialize kappa in the paper, one based on a fixed value, one on the initialization of the parameter group, and one after a fixed number of training steps. Please find the algorithm below:

Experiments
We provide empirical evidence of CPR’s effectiveness through multiple experiments in the paper. We present here the performance in modular addition, image classification, and language modeling.
Modular Addition
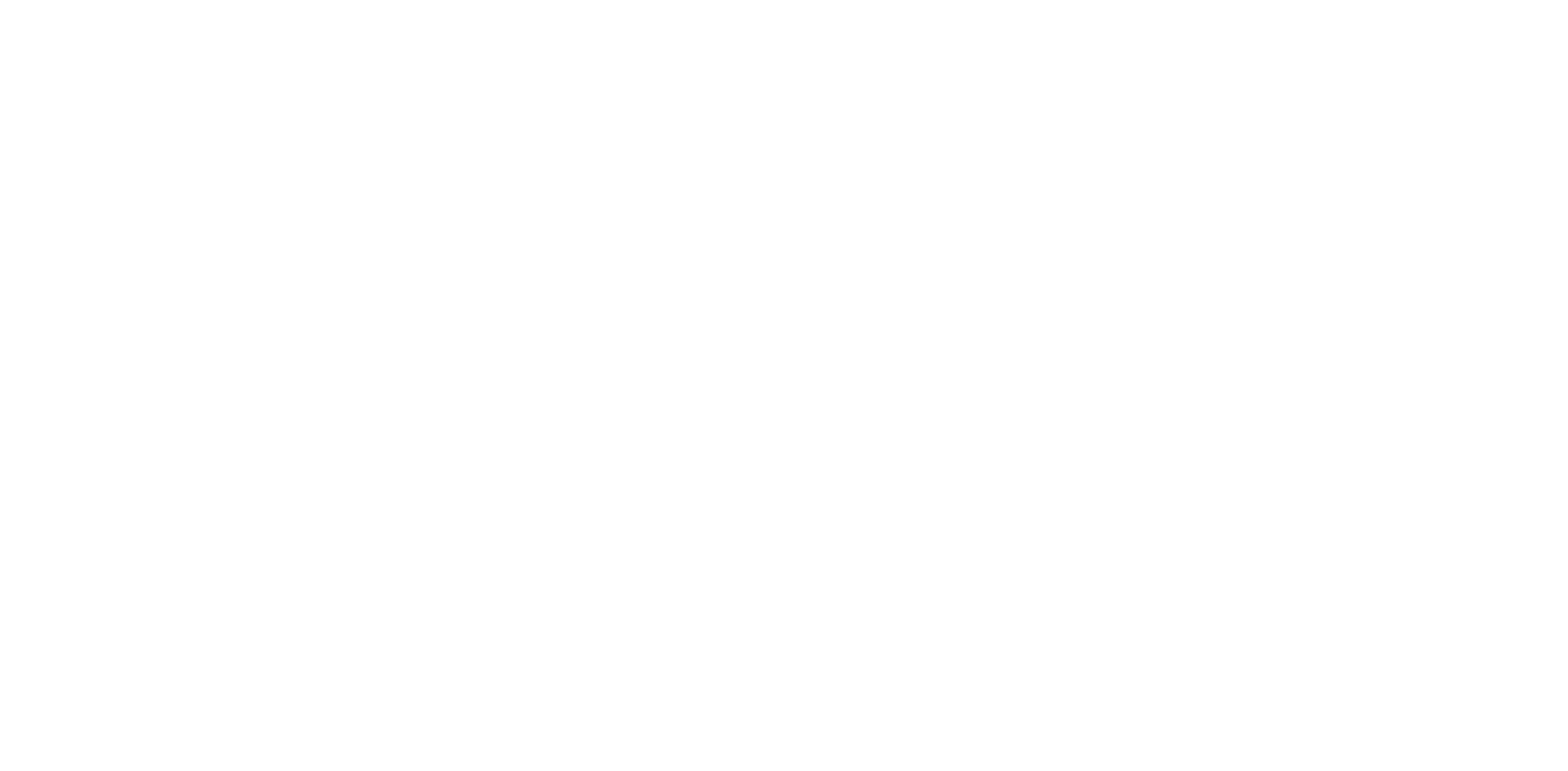
The first experiment focuses on the modular addition task, where CPR demonstrates its ability to counteract the “grokking” phenomenon. We use in this experiment AdaCPR, which is CPR with an adaptive kappa bound. The results in the figure below reveal that AdaCPR nearly mitigates the effects of grokking and achieves faster convergence.
The figure shows experiments on the modular addition task to illustrate the effect of AdaCPR. The training steps on the x-axis are displayed in the log scale. The training and validation accuracy are displayed in red and blue. In the middle row, we see the standard deviation of the attention-in-weight parameter during the training progress and at the bottom the mean L2 norm. In the left column, we use AdamW for optimization with a weight decay of 1.0, and in the middle and right columns Adam with AdaCPR. On the left side, we see the λ value during training and the dotted black line represents the upper bound κ. We optimize in the middle to a standard deviation of k = 0.9 times the initial value and on the right to an L2 norm with k = 0.8.
Image Classification
In the domain of image classification, CPR was tested with ResNet18 on the CIFAR100 dataset.
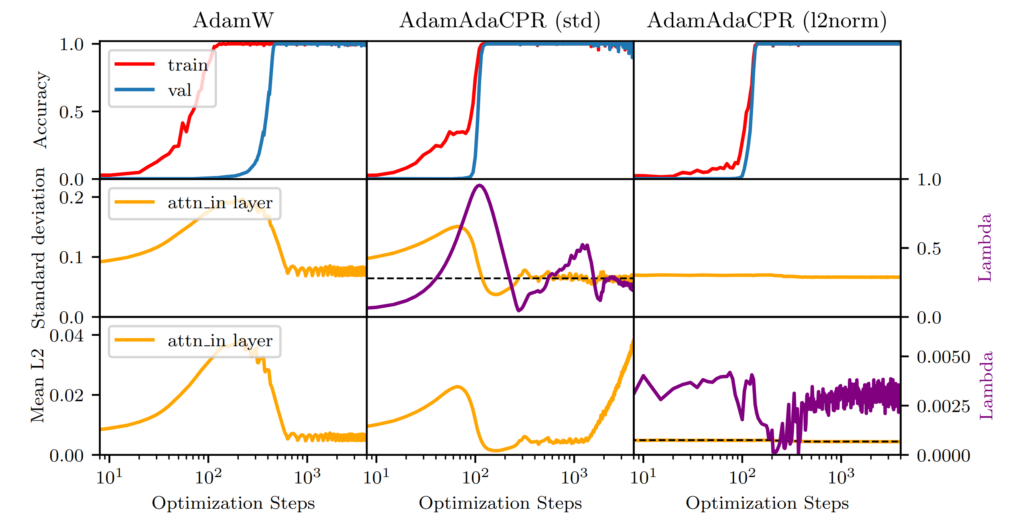
Here, CPR, especially when using the L2-norm as a regularization function, outperformed traditional methods, showcasing its effectiveness in vision tasks. The figure shows the percentage of correct labels of a model trained with AdamW and AdamCPR on different learning rates and regularization hyperparameters in the figure below.
AdamCPR uses the L2 norm as a regularization function and initializes the upper bound after k training steps. We see that AdamCPR achieves better results than AdamW for all learning rates.
The best results are achieved when initializing kappa after 1000 training steps.
Language Modeling
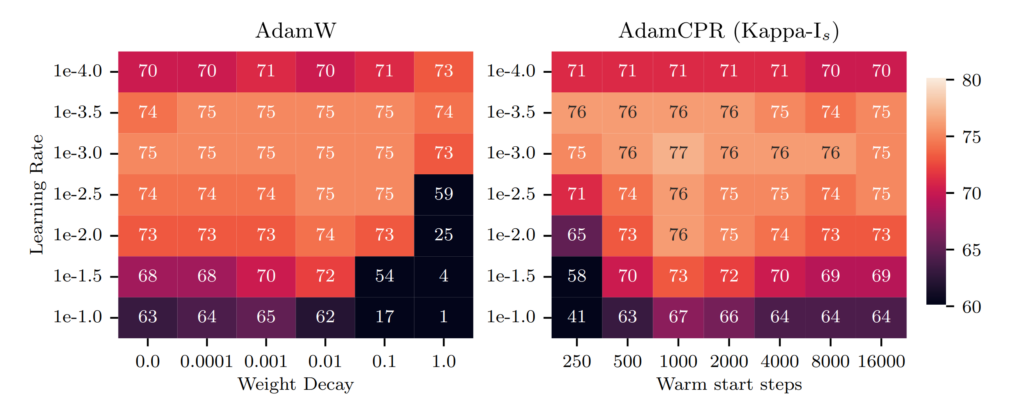
In our language modeling experiment, CPR was applied to a GPT2s model trained on the OpenWebText dataset. The experiment highlighted CPR’s ability to perform well on mid-scale language modeling tasks.
The mean validation PPL of three runs (±std as shaded area) with AdamW and the CPR (Kappa init after k stepsIs) are displayed in blue and green below:
We see the learning curves of the best AdamW and best AdamCPR run and we can observe that weight decay regularizes the model less strongly in the early stages of training which may lead to a better final
performance.
Conclusion
CPR marks a significant advancement in the field of deep learning regularization. Its ability to adaptively and dynamically regularize diverse parameter groups in a neural network addresses the limitations of traditional methods. This research not only contributes a novel approach to regularization but also opens avenues for more robust and efficient neural network training across various applications.
For a deeper exploration and comprehensive experiments, please read the full preprint.
This work will be presented at the NeurIPS 2023 workshop on optimization for machine learning (OPT2023).